میدان الکتریکی (Electric Field) چیست؟

نیروهای وارد شده به مجوعه‌ای از ذرات بحث کردیم. این که یک ذره به موجودات اطراف خود چه نیرویی وارد می‌کند، به جرم اطراف وابسته است. اما آیا به راستی می‌توان خاصیتی تعریف کرد که توانایی هر ذره را در تولید نیرو بدون در نظر گرفتن بار ذرات اطراف بیان کند. در این قسمت قصد داریم تا در مورد چنین مفهومی صحبت کنیم.

تعریف میدان الکتریکی

نیرو‌های الکترواستاتیکی همانند نیروی گرانشی در امتداد یه خط مستقیم عمل می‌کنند. این نیروها حتی در زمانی که دو ذره در تماس با یکدیگر نباشند، نیز وجود دارند. برای توضیح این پدیده، مفهومی تحت عنوان میدان الکتریکی تعریف می‌شود. میدان الکتریکی خاصیتی است که هر بار الکتریکی در اطراف خود ایجاد می‌کند.

برای بدست آوردن اندازه و مقدار این خاصیت از جزئی فرضی تحت عنوان بار آزمون استفاده می‌شود. این بار در حقیقت موجودی است که میدان الکتریکی ایجاد شده توسط بار q را حس می‌کند. میدان الکتریکی، برداری فیزیکی اطراف یک بار است که با استفاده از عبارت زیر تعریف می‌شود.

به منظور تاثیر نگذاشتن بر میدان ناشی از q، بار q_۰ به اندازه بینهایت کوچک فرض شده. شبیه‌سازی بین میدان گرانشی دو جرم و میدان الکتریکی دو بار، در شکل زیر نشان داده شده است.

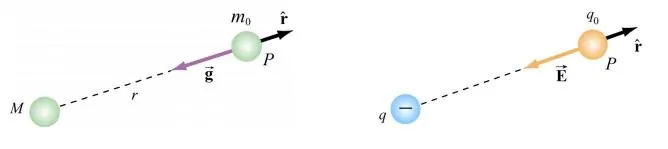
در حقیقت میدان گرانشی را می‌توان هم‌چون میدان الکتریکی، با استفاده از فرمول زیر بیان کرد:

از این رو می‌توان گفت: «بار q میدان E را در اطراف خود ایجاد کرده و نیروی Eq_۰ را به ذره q_۰ وارد می‌کند.»

با استفاده از قانون جمع آثار میدان الکتریکی ناشی از مجموعه‌ای از ذرات را می‌توان با استفاده از جمع برداری میدان‌ها و در قالب سری زیر بیان کرد.

رابطه بالا دقیقا همان‌ مفهومی است که در مطلب قانون کولن در مورد نیروهای وارد شده به مجموعه‌ای از ذرات شرح داده شد.

خطوط میدان الکتریکی

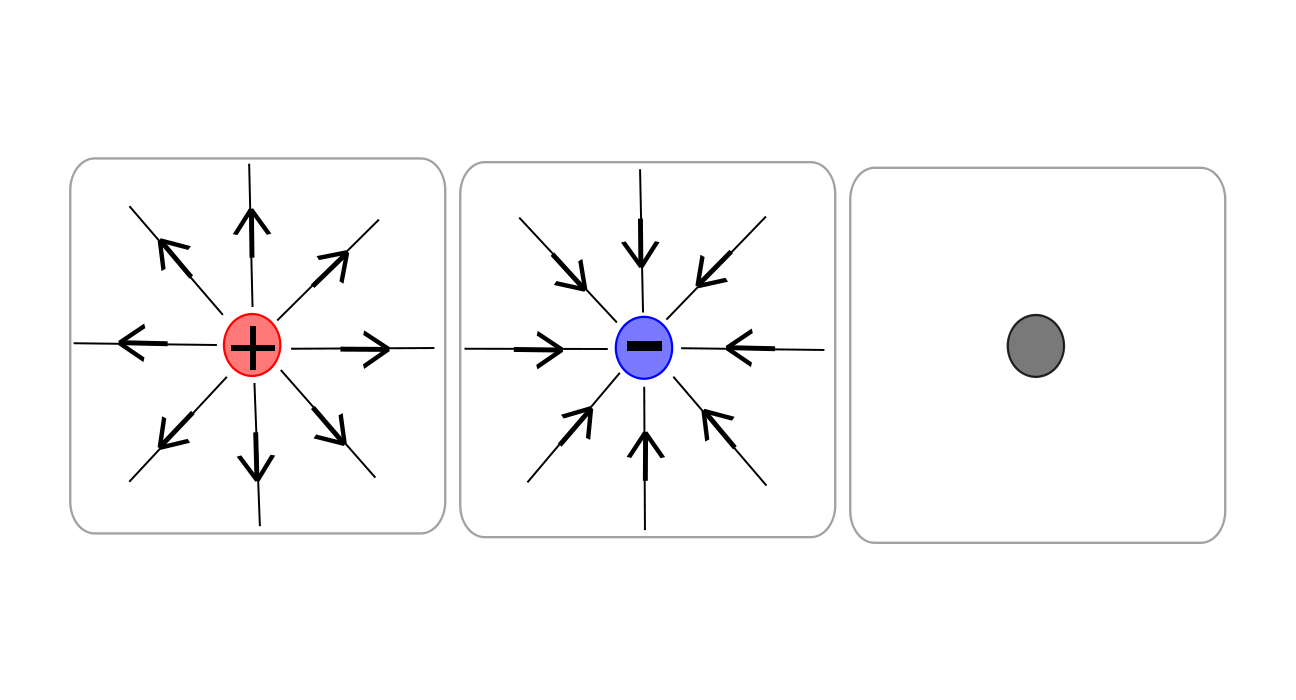
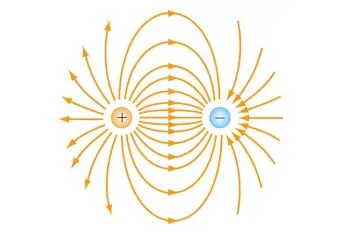
ابتدایی‌ترین روش برای نشان دادن میدان الکتریکی، استفاده از خطوط میدان است. با بکارگیری این خطوط، می‌توان به توصیف درستی از وضعیت میدان الکتریکی در فضا دست یافت. شکل زیر خطوط میدان الکتریکی را برای دو ذره با بار مثبت و منفی نشان می‌دهند.

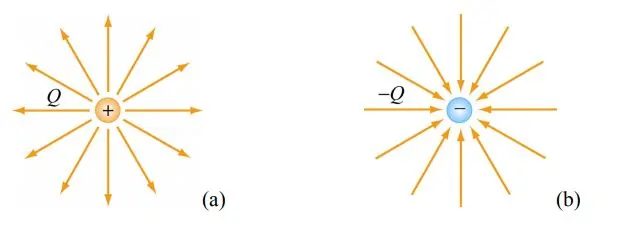
همان‌طور که در شکل بالا نیز مشخص است، خطوط میدان الکتریکی برای ذرات با بار مثبت به صورت شعاعی دورشونده و همین خطوط برای ذرات با بار منفی به صورت نزدیک‌ شونده هستند. این خطوط برای ذراتی با اندازه برابر و علامت مخالف، به شکل زیر هستند.

جهت تعیین الگوی خطوط میدان می‌توان نکات زیر را مد نظر قرار داد.

1. تقارن: اگر دو بار را با استفاده از یک خط به هم وصل کنیم، الگوی میدان الکتریکی بایستی نسبت به این خط متقارن باشد.
2. میدان نزدیک بار: هنگامی که به اندازه کافی به یک ذره نزدیک می‌شویم، میدان ناشی از آن نسبت به میدان‌های دیگر ذرات، بسیار بزرگ‌تر است. در نتیجه خطوط میدان الکتریکی نزدیک یک بار به صورت کروی در نظر گرفته می‌شوند.
3. میدان دور از بار: در فاصله‌ای بسیار دور از مجموعه‌ای از بارها، خطوط میدان را می‌توان ناشی از یک بار به اندازه $$Q=\sum Q_i$$

3. در نظر گرفت.

در حالت کلی می‌توان ویژگی‌های زیر را برای خطوط میدان تعریف کرد.

1. جهت میدان الکتریکی در یک نقطه برابر با بردار مماس بر خطوط میدان در آن نقطه در نظر گرفته می‌شود.
2. تعداد خطوطِ میدان در واحد سطح، در  صفحه عمود بر خطوط، نشان‌دهنده قدرت میدان در صفحه مد نظر است.
3. خطوط میدان از ذرات با بار مثبت شروع شده و به ذرات با بار منفی ختم می‌شوند.
4. تعداد خطوطی که از بار مثبت خارج و یا به بار منفی وارد می‌شوند، نشان‌دهنده اندازه بارهای الکتریکی مذکور هستند.
5. دو خط میدان الکتریکی،‌ هیچ‌گاه همدیگر را قطع نخواهند کرد.

نیروی اعمال شده به ذره قرار گرفته در میدان الکتریکی

مطابق با شکل زیر فرض کنید که بار مثبت q بین دو صفحه با بار مخالف در حال حرکت است.

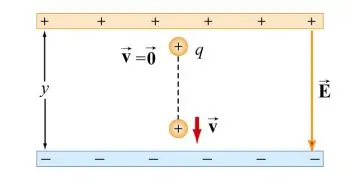
همان‌طور که از شکل بالا نیز پیدا است، میدان ناشی از این بار‌ها تنها در جهت y هستند. از این رو می‌توان گفت:

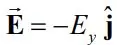
در بالا گفتیم که هرگاه باری در میدان الکتریکی قرار گیرد، میدان مذکور به آن نیرو وارد می‌کند. بنابراین در حالت کلی نیروی وارد شده به بار q که در میدان E قرار گرفته برابر است با:

$$\overrightarrow{F}=\overrightarrow{E}q$$

توجه داشته باشید که در این مثال بار q میدان ناشی از بار‌هایی را تجربه می‌کند که روی صفحات قرار گرفته‌اند. البته شاید این سوال را در ذهن داشته باشید که نیروی ناشی از میدان خود ذره q لحاظ می‌شود؟ پاسخ این سوال منفی است چراکه با توجه به قانون سوم نیوتن بار q به خود نیرویی وارد نمی‌کند. از طرفی با استفاده از قانون دوم نیوتن می‌توان شتاب وارد شده به ذره را به شکل بدست آورد.

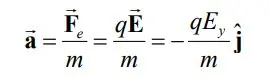
به نظر شما سرعت ذره در لحظه رسیدن به صفحه دوم چقدر است؟

با بکارگیری معادلات گالیله، سرعت ذره در لحظه رسیدن به صفحه دوم را می‌توان بشکل زیر بدست آورد.

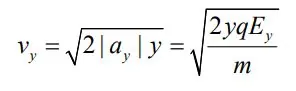
جالب است بدانید که انرژی جنبشی ذره در لحظه رسیدن به صفحه پایین، برابر است با:

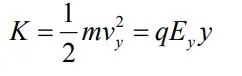
بدست آوردن میدان الکتریکی نیز دقیقا همانند محاسبه نیرو است. در حقیقت میدان ناشی از مجموعه‌ای از بارهای الکتریکی، در نقطه‌ای از فضا را می‌توان با استفاده از برآیند میدان‌های تک‌تک ذرات بدست آورد. برای درک بهتر به مثال‌ ارائه شده در ادامه توجه کنید.

مثال ۱

مطابق شکل زیر دو بار q_a و q_b در فاصله c از یکدیگر قرار گرفته‌اند. تصور کنید که دقیقا در وسط این دو بار، بار جدید q_c را قرار می‌دهیم.

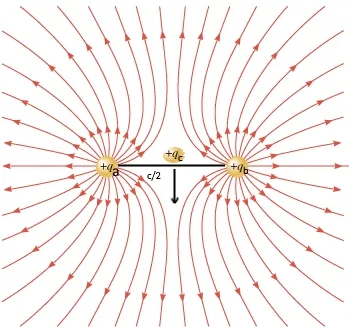
در این حالت نیروی وارد شده به بار q_c چقدر است؟ بار‌ها و فواصل در این مسئله به شرح زیر هستند.

$$q_a=\mathrm{۵۰}\mu C,q_b=\mathrm{۱۰۰}\mu C,q_c=\mathrm{۲۰}\mu C,c=\mathrm{۱.۰}m$$

با توجه به مفاهیم بیان شده در قانون کولن، می‌توان نیروی ناشی از بار‌های a و b را به صورت جداگانه روی ذره c محاسبه کرد. اما روش آسان‌تر این است که میدان الکتریکی را در نقطه c محاسبه کنیم و با قرار دادن بار c در آن نقطه، نیروی وارد به بار را بدست آوریم. بنابراین میدان الکتریکی ناشی از بار‌های q_a و q_b به ترتیب برابر هستند با:

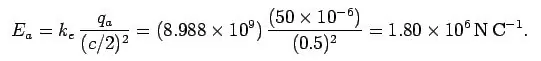
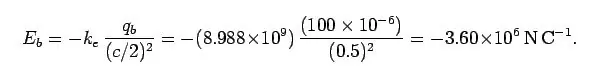
در نتیجه برآیند میدان الکتریکی در نقطه c را می‌توان به شکل زیر بدست آورد.

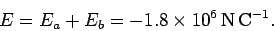
علامت منفی پشت میدان الکتریکی نشان دهنده این است که میدان الکتریکی برآیند در این نقطه در خلاف جهت محور x است. با استفاده از فرمول F=Eq می‌توان نیروی وارد شده به بار c را به صورت زیر محاسبه کرد.

توجه داشته باشید که در محاسبه نیروی ناشی از میدان روی یک ذره، بایستی علامت بار و علامت میدان را اعمال کرد.

توزیع پیوسته بار‌های الکتریکی

در واقعیت معمولا میدان الکتریکی ناشی از توزیع پیوسته‌ای از بار مورد بررسی قرار می‌گیرد. در چنین مسائلی در ابتدا میدان ناشی از دیفرانسیلی از بار را محاسبه کرده و پس از آن با استفاده از انتگرال‌گیری، میدان تمامی بارها را محاسبه می‌کنیم. در حقیقت باری به اندازه dq را در نظر می‌گیریم و میدان ناشی از آن را بدست می‌آوریم. در شکل زیر دیفرانسیل بار و میدان الکتریکی ناشی از این جزء نشان داده شده.

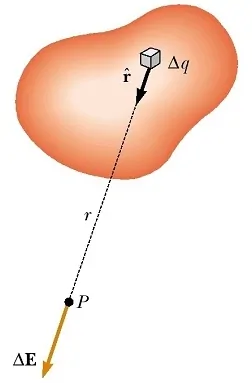
مهم‌ترین نکته در این روش یافتن رابطه‌ای منظم بین بار‌ها و میدان الکتریکی به نحوی است که امکان انتگرال‌گیری وجود داشته باشد. به‌منظور محاسبه میدان ناشی از توزیع پیوسته‌ای از بار‌های الکتریکی در ابتدا نیاز داریم تا مفهومی تحت عنوان «چگالی بار» (Charge Density) را تعریف کنیم.

چگالی بار

همان‌طور که در بالا نیز بیان شد، میدان الکتریکی ناشی از تعدادی بار الکتریکی را می‌توان با استفاده از روش جمع آثار بدست آورد. معمولا توزیع‌های پیوسته بار الکتریکی، در قالب مفاهیمی هم‌چون چگالی حجمی، سطحی و یا خطی بار الکتریکی بیان می‌شود.

چگالی حجمی بار الکتریکی

شکل زیر توزیع حجمی پیوسته‌ای از بارهای الکتریکی را نشان می‌دهد. بدیهی است که این توزیع،‌ میدانی الکتریکی را در نقطه دلخواه P ایجاد خواهد کرد.

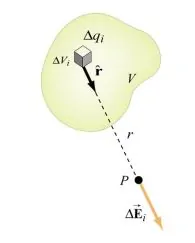
از این رو در ابتدا جزء حجمی به اندازه $$\Delta V_i$$

را در نظر بگیرید. همان‌طور که می‌دانید این جزء شامل باری الکتریکی است که آن را با $$\Delta q_i$$

نشان می‌دهیم. با این فرضیات چگالی حجمی بار الکتریکی که تابعی از بردار r است را می‌توان به شکل زیر بیان کرد:

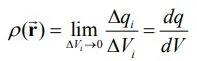
در سیستم SI واحد کمیت تعریف شده در بالا برابر با C/m^۳ است. با توجه به رابطه بالا کلِ بارهای موجود در یک سیستم را می‌توان با استفاده از انتگرال‌گیری زیر محاسبه کرد.

برای درک بهتر چگالی بار الکتریکی می‌توانید از مفهوم چگالی جرمی استفاده کنید. در حقیقت عبارت زیر، معادل با رابطه بالا برای حالتی است که می‌خواهیم جرم کل یک سیستم را محاسبه کنیم.

چگالی سطحی بارهای الکتریکی

مشابه با حالت حجمی، در حالت مواجه با مسئله‌ای دوبعدی، می‌توان از مفهوم چگالی سطحی بار الکتریکی استفاده کرد. از این رو چگالی سطحی سیستمی با مساحت سطح A و بار q با استفاده از رابطه زیر تعریف می‌شود.

واحد σ در سیستم SI برابر با C/m^۲ است. با استفاده از تعریف چگالی سطحی، بار کل موجود در یک سطح دوبعدی را می‌توان به شکل زیر محاسبه کرد.

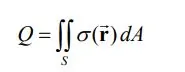
چگالی خطی بارهای الکتریکی

میله‌ای به طول l را تصور کنید که حاوی باری الکتریکی به اندازه q است. برای این میله چگالی خطی به شکل زیر محاسبه می‌شود.

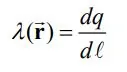
واحد λ در SI برابر با C/m است. با توجه به تعریف انجام شده،‌ می‌توان کل بار موجود در یک سیستم یک بعدی را با استفاده از انتگرال زیر بدست آورد.

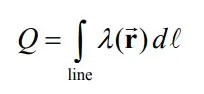
معمولا توزیع بار در مسائل را به صورت یکنواخت در نظر می‌گیرند. در حقیقت اعداد ρ ،σ و λ برابر با مقادیری ثابت در تمامی دامنه توزیع بار در نظر گرفته می‌شوند. حال با توجه به تعریف مفهوم چگالی، قادریم تا میدان الکتریکی ناشی از توزیع پیوسته بار‌های الکتریکی را محاسبه کنیم.

میدان الکتریکی ناشی از توزیع پیوسته بارهای الکتریکی

برای محاسبه میدان الکتریکی در ابتدا میدان ناشی از بار جزئی dq را با استفاده از رابطه زیر بیان می‌کنیم.

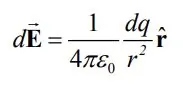
بدیهی است که به منظور محاسبه میدان کل، بایستی از رابطه بالا،‌ در تمامی دامنه انتگرال گرفت. برای نمونه میدان ناشی از توزیع حجمی بار الکتریکی را می‌توان به صورت زیر بدست آورد.

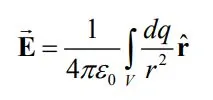
برای درک بهتر مفهوم توزیع بار‌های الکتریکی، توجه شما را به مثال‌های زیر جلب می‌کنیم.

مثال ۲

مطابق شکل زیر میله‌ای به طول L را تصور کنید که باری برابر با q- در خود نگه داشته است. فرض کنید که توزیع بار در این میله به صورت کاملا یکنواخت باشد. میدان الکتریکی در فاصله a از لبه سمت راست میله چقدر است؟

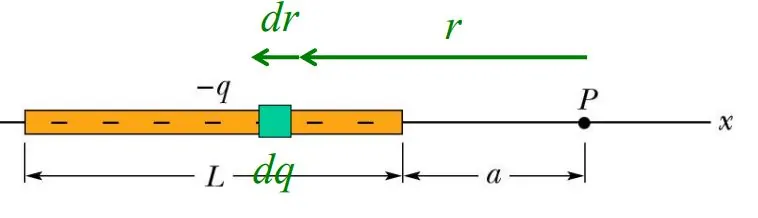
همان‌طور که در بالا گفتیم، برای حل چنین مسائلی در ابتدا بایستی الگویی برای توزیع بار تعریف کنیم. از آنجایی که در این مسئله بار به صورت یکنواخت در میله توزیع شده، بنابراین می‌توان چگالی خطی بار الکتریکی را به صورت زیر تعریف کرد.

در مرحله دوم بخشی کوچک از میله را در نظر می‌گیریم و میدان الکتریکی ناشی از آن را محاسبه می‌کنیم. بنابراین با توجه به چگالی تعریف شده، داریم:

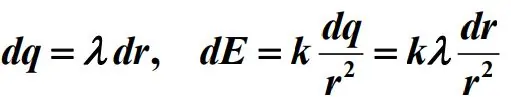
با توجه به مختصات تعریف شده برای r، بایستی انتگرال dE را از a تا a+L محاسبه کرد. بنابراین می‌توان گفت:

البته در بعضی از موارد راحت‌تر است که انتگرال را در مختصات استوانه‌ای یا کروی بدست آوریم. در مثال زیر از مختصات استوانه‌ای به‌منظور محاسبه میدان ناشی از حلقه‌ای باردار استفاده شده است.

مثال ۳

همانند شکل زیر فرض کنید بار Q به شکلی یکنواخت روی حقله‌ای توزیع شده. در این صورت میدان ناشی از این توزیع در فاصله z از حلقه را بیابید.

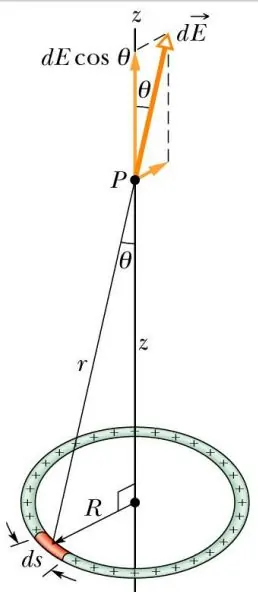
شکل ۱

از آنجایی که توزیع بار به صورت یکنواخت در نظر گرفته شده، بنابراین می‌توان جزء بار الکتریکی و دیفرانسیل میدان ناشی از آن را به صورت زیر محاسبه کرد.

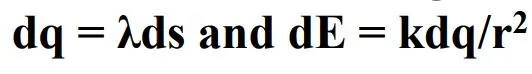
از آنجایی که سیستم متقارن است بنابراین مولفه‌های x و y میدان یکدیگر را خنثی کرده و فقط این مولفه z است که وجود خواهد داشت. در نتیجه می‌توان گفت که تنها دیفرانسیل زیر است که غیر صفر خواهد بود.

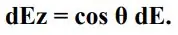
با انتگرال‌گیری از رابطه بالا میدان الکتریکی برابر می‌شود با:

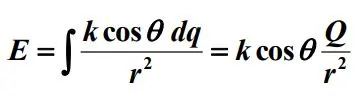
با توجه به شکل ۱ مقدار cos θ را می‌توان با استفاده از رابطه زیر بدست آورد.

با جایگذاری cos θ در رابطه ۱، نهایتا میدان الکتریکی برابر با مقدار زیر بدست می‌آید.

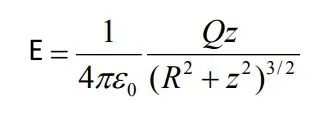
رابطه بالا بیان می‌کند که میدان یک دیسک به صورت پیوسته کم نمی‌شود. در حقیقت در ابتدا اندازه میدان به یک مقدار ماکزیمم رسیده و پس از آن کاهش می‌یابد. نمودار زیر تغییرات اندازه میدان الکتریکی را بر حسب فاصله از دیسک نشان می‌دهد.

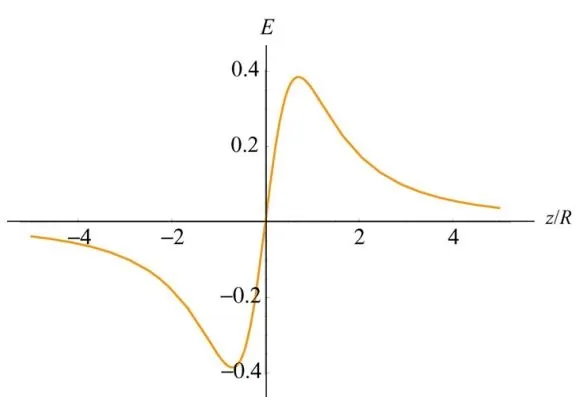
شاید قبل از بدست آوردن میدان الکتریکی این احساس را داشته باشیم که با دور شدن از دیسک،‌ میدان الکتریکی به‌صورت پیوسته کم می‌شود. مثالی که در ادامه آمده، نمونه‌ای مناسب برای درک مفهوم میدان الکتریکی ناشی از توزیع سطحی بار الکتریکی است.

مثال ۴

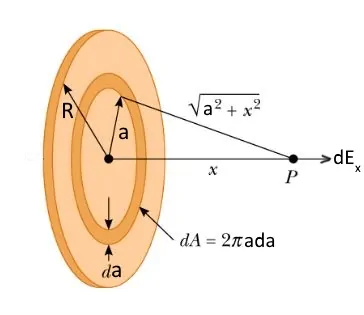
مطابق با شکل زیر فرض کنید، می‌خواهیم میدان الکتریکی ناشی از توزیع بار Q روی دیسکی به شعاع R را در فاصله x از دیسک محاسبه کنیم.

با توجه به یکنواخت بودن توزیع بار، چگالی سطحی بار الکتریکی برابر با مقدار زیر تعریف می‌شود.

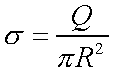
برای محاسبه میدان، در اولین قدم حلقه‌ای به ضخامت دیفرانسیلی da را مطابق با شکل ۲ در نظر می‌گیریم؛ پس از آن میدان دیفرانسیلی ناشی از آن را محاسبه کرده و نهایتا با انتگرال‌گیری روی کل دیسک، میدان الکتریکی کل نیز بدست خواهد آمد. مساحت حلقه کوچک در نظر گرفته شده، برابر است با:

این حلقه حاوی باری به اندازه زیر است.

بار جزئی محاسبه شده در بالا،‌ منجر به میدانی جزئی در فاصله x از خود می‌شود. اندازه میدان جزئی برابر است با:

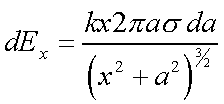
نهایتا با استفاده از انتگرال‌گیریِ رابطه بالا از a=0 تا a=R، میدان الکتریکی برابر با مقدار زیر بدست می‌آید.

حاصل انتگرال بالا را می‌توان با استفاده از روش تغییر متغیر محاسبه کرد. پس از محاسبه انتگرال، میدان الکتریکی ناشی از دیسک، در فاصله x از آن به صورت زیر بدست می‌آید.

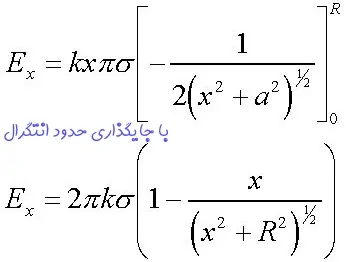
در حالت عمومی می‌توان توزیع‌های مختلفی از بار‌ را روی یک سیستم فرض کرد. هم‌چنین مثال‌های بالا مقدمه‌ای برای توصیف میدان‌های پیچیده‌تر هستند.

دوقطبی الکتریکی

به مجموعه دو ذره با بار برابر و علامت مخالف، دوقطبی الکتریکی گفته می‌شود. برای نمونه شکل زیر دو بار q+ و q- را نشان می‌دهد که در فاصله ۲a از یکدیگر قرار گرفته‌ و یک دوقطبی را تشکیل می‌دهند.

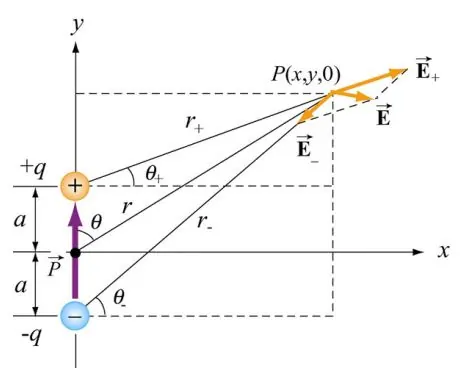
برای سیستمی مطابق شکل بالا، کمیتی برداری تحت عنوان $$\overrightarrow{p}$$

تعریف می‌شود که مقدار آن در قالب فرمول زیر تعریف می‌شود.

$$\overrightarrow{p}=\mathrm{۲}qa\hat{j}$$

در رابطه بالا ۲qa را اندازه دوقطبی می‌نامند. در حالت عمومی، برای یک سیستم متشکل از N بار، بردار دوقطبی الکتریکی را می‌توان به شکل زیر تعریف کرد.

در رابطه بالا $${\overrightarrow{r}}_i$$

بردار مکان بار q_i را نشان می‌دهد. مولکول‌های شناخته شده‌ای مثل HCL ،CO و H_۲O بهترین نمونه‌های دوقطبی الکتریکی هستند. در حالت کلی هر مولکولی که مرکز مثبت و منفی آن بر یکدیگر منطبق نباشد را می‌توان به عنوان یک دوقطبی الکتریکی تلقی کرد.

میدان الکتریکی یک دوقطبی

شاید این سئوال برایتان پیش آمده باشد که چطور می‌توان میدان الکتریکی ناشی از یک دوقطبی را محاسبه کرد؟ بر مبنای شکل ۳ اندازه میدان الکتریکی در نقطه P و در راستای x برابر با مقدار زیر است.

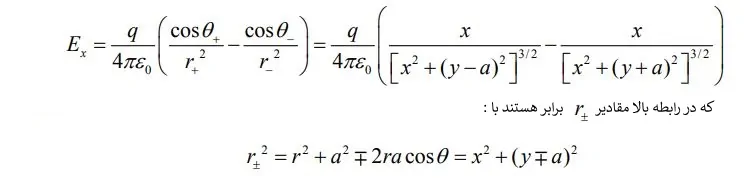
مشابه با حالت بالا، میدان الکتریکی این دوقطبی در راستای y را می‌توان با استفاده از رابطه زیر بدست آورد.

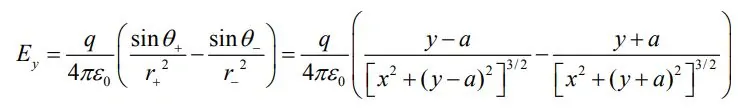
در حالتی که فاصله r را بسیار بزرگ‌تر از a در نظر بگیریم، مولفه‌های x و y میدان الکتریکی به صورت زیر در می‌آیند.

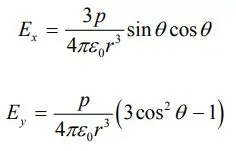
در رابطه بالا sin θ=x/r و cos θ=y/r محاسبه می‌شوند. در نتیجه رابطه $$\mathrm{۳}prcos\theta =\mathrm{۳}\overrightarrow{p}.\overrightarrow{r}$$

برقرار است. نهایتا میدان الکتریکی را می‌توان بر حسب ضرب داخلی بردار گشتاور دوقطبی  و موقعیت ذره، به شکل زیر بیان کرد:

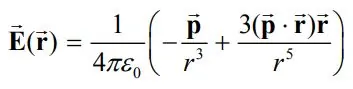
معادله بالا در حالت سه‌بعدی نیز قابل بیان است. هم‌چنین این رابطه نشان می‌دهد که با افزایش r میدان الکتریکی $$\overrightarrow{E}$$

کاهش می‌یابد. به حالتی که دو بار مثبت و منفی q بسیار به هم‌ نزدیک باشند، بار نقطه‌ای گفته می‌شود. در شکل زیر میدان ناشی از دو بار در دو حالت نقطه‌ای و حالتی که با هم فاصله داشته باشند‌، نشان داده شده.

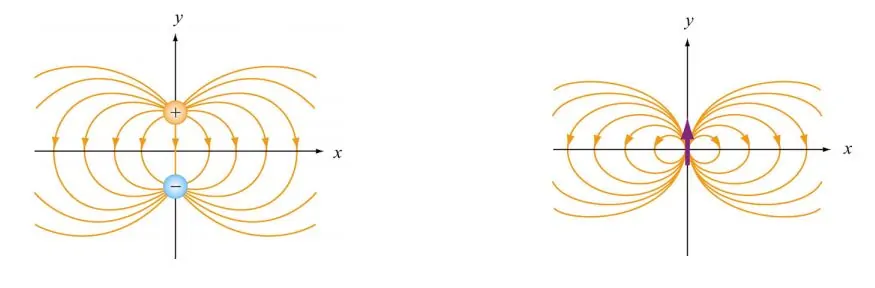
حضور دوقطبی در میدان الکتریکی

به نظر شما اگر یک دوقطبی با گشتاور $$\overrightarrow{P}$$

در معرض میدانی در راستای x قرار گیرد، چه اتفاقی خواهد افتاد. برای بررسی این موضوع، مطابق با شکل زیر، دو قطبی را در نظر بگیرید که در یک میدان الکتریکی قرار گرفته.

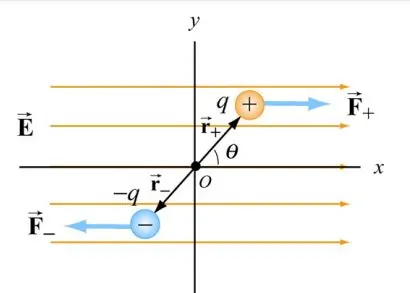
با فرض این‌که زاویه بردار گشتاور آن با محور x برابر با $$\theta$$

باشد، می‌توان گفت:

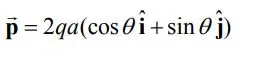
همان‌طور که از شکل ۴ نیز مشخص است، از آنجایی که نیروی برابر ولی با جهت مخالف به دو قطبی وارد می‌شود، بنابراین نیروی خالص وارد شده به مجموعه دوبار برابر با صفر است. در نتیجه می‌توان نوشت:

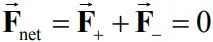
اگرچه برآیند این نیروها صفر است، اما منجر به ایجاد گشتاور خالصی حول نقطه O خواهند شد. این گشتاور به شکل زیر بدست می‌آید.

$$F_{-}$$

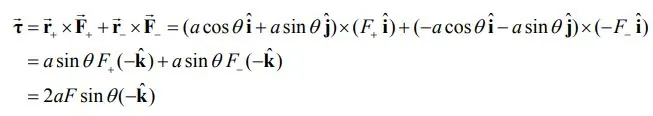
نیروی وارد به بار منفی و $$F_{+}$$

نیروی وارد به بار مثبت را نشان می‌دهد. با بررسی رابطه بالا متوجه می‌شویم که جهت گشتاور خلاف جهت محور عمود بر صفحه است. این گشتاور منجر به دوران ساعتگرد دوقطبی شده و بردار‌ میدان و گشتاور دوقطبی را با یکدیگر هم‌جهت می‌کند. با استفاده از رابطه F=Eq، اندازه گشتاور وارد شده به دو قطبی را می‌توان از رابطه زیر محاسبه کرد.

فرم عمومی رابطه بالا را به‌شکل زیر بیان می‌شود:

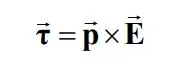
رابطه بالا حاصلضرب خارجی تکانه خطی یک دوقطبی در میدان الکتریکی است. مفهوم دوقطبی بیشتر به‌منظور توضیح رفتار مولکو‌ل‌ها مورد استفاده قرار می‌گیرد. در آینده در مورد کاربرد دوقطبی الکتریکی بیشتر بحث خواهیم کرد.