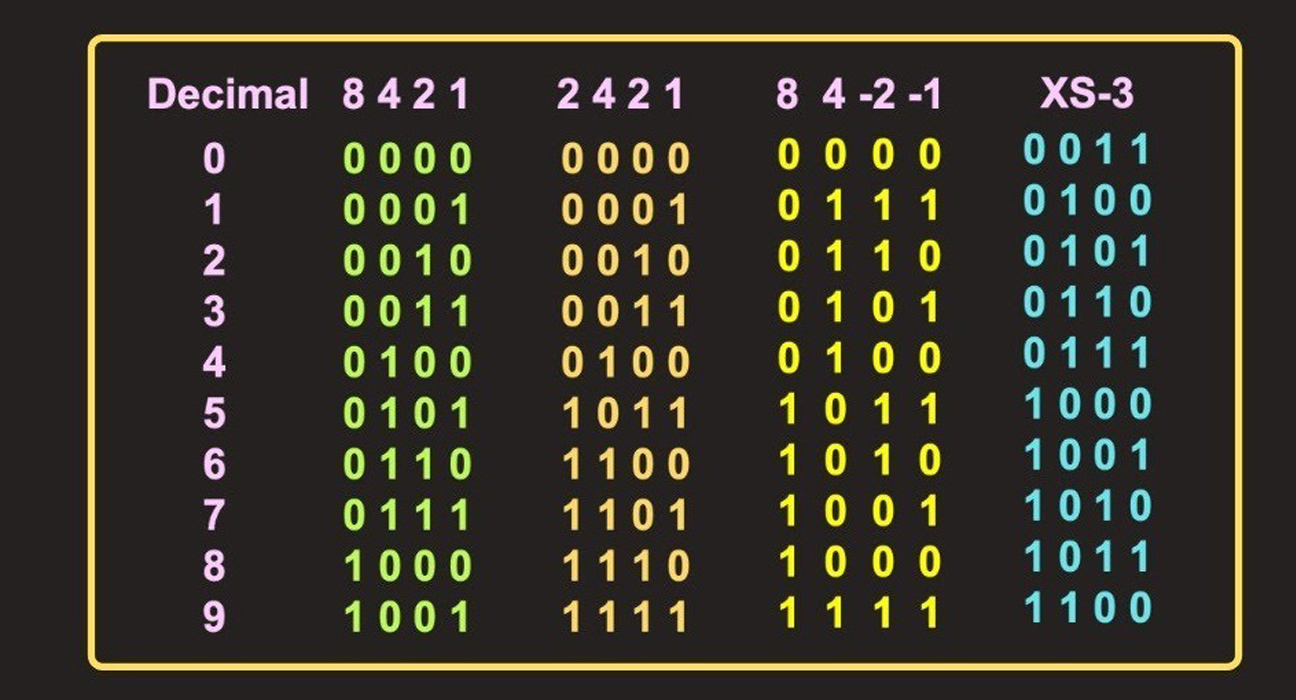
«دهدهی کد شده به باینری» یا کد Binary Coded Decimal) BCD) روشی برای تبدیل اعداد دهدهی به معادل باینری آنهاست. همانگونه که در آموزش نخست اعداد باینری دیدیم، در مدارهای الکتریکی و دیجیتالی از کدهای باینری مختلفی استفاده میشود که هرکدام کاربرد خاص خود را دارند.
از آنجایی که در محاسبات روزمره از اعداد مبنای ۱۰ یا دهدهی استفاده میشود اما کامپیوترها و دستگاههای دیجیتالی تنها اعداد باینری را درک میکنند، به روشی نیاز داریم که اعداد دهدهی را به باینری یا مبنای ۲ تبدیل کنیم. استفاده از کد BCD یکی از بهترین روشها برای این کار است.
همانطور که میدانیم یک کد باینری n بیتی، مجموعهای از n بیت است که با آن میتوان تا ۲n ترکیب متمایز ایجاد کرد. مزیت استفاده از سیستم BCD در این است که همانند سیستم هگزادسیمال، هر رقم دهدهی نمایندهی ۴ بیت است؛ لذا برای نمایش هر رقم دهدهی (۰ تا ۹) از یک کد باینری چهار بیتی استفاده میشود.
البته کدهای BCD دقیقاً مانند اعداد هگزادسیمال نیستند و تفاوتهایی نیز وجود دارد. به عنوان مثال، حداکثر مقداری که یک عدد هگزادسیمال چهار بیتی میتواند اختیار کند F۱۶ یا ۱۱۱۱۲ است که معادل ۱۵ دهدهی است. اما یک کد BCD حداکثر میتواند تا عدد ۹ یا ۱۰۰۱۲ باشد. این مسئله بدان معنی است که با وجود اینکه با چهار رقم باینری میتوان تا ۱۶ عدد را نشان داد (۲۴)، اما در سیستم شمارش BCD شش ترکیب آخر کاربردی ندارند؛ یعنی استفاده از اعداد ۱۰۱۰ (۱۰ دهدهی)، ۱۰۱۱ (۱۱ دهدهی)، ۱۱۰۰ (۱۲ دهدهی)، ۱۱۰۱ (۱۳ دهدهی)، ۱۱۱۰ (۱۴ دهدهی) و ۱۱۱۱ (۱۵ دهدهی) ممنوع است.
بزرگترین مزیت استفاده از کد BCD، راحتتر کردن تبدیل اعداد باینری و دهدهی به یکدیگر است. اگرچه کد BCD بدیهایی نیز دارد که مهمترین آن، عدم استفاده از اعداد ۱۰۱۰ (۱۰ دهدهی) تا ۱۱۱۱ (۱۵ دهدهی) است. با این وجود کد BCD کاربردهای بسیار مهمی مخصوصاً در نمایشدهندههای دیجیتال دارد.
در سیستم شمارهگذاری BCD، هر رقم از اعداد دهدهی به چهار بیت تقسیم میشود. برای ساخت یک کد BCD، تنها کافی است معادل باینری هر رقم دهدهی را در قالب چهار بیتی بنویسیم. لذا یک گروه چهار بیتی ۱۰ حالت مختلف خواهد داشت که از ۰۰۰۰ برای صفر تا ۱۰۰۱ برای نه را شامل میشود.
به عنوان مثال، عدد دهدهی ۳۵۷۱۰ در کد BCD به شکل زیر نمایش داده میشود:
۳۵۷۱۰ = ۰۰۱۱ ۰۱۰۱ ۰۱۱۱ (BCD)
همانگونه که میبینیم، در سیستم BCD از «کدگذاری وزنی» استفاده میشود، زیرا جایگاه هر گروه چهار بیتی، وزنی دارد که در مقدار نهایی تأثیرگذار است. به عبارت دیگر، BCD یک کد وزندار است و وزنهای استفاده شده در کد BCD عبارتند از ۸، ۴، ۲ و ۱. لذا از آنجایی که کد BCD نشاندهندهی معادل باینری رقم دهدهی مربوطه است، عموماً به آن «کد ۸۴۲۱» نیز گفته میشود.
نمایش کد BCD یک عدد دهدهی
| ۲۰ | ۲۱ | ۲۲ | ۲۳ | توان باینری |
| ۱ | ۲ | ۴ | ۸ | وزن باینری |
در اعداد دهدهی با حرکت به سمت چپ، وزن هر رقم دهدهی با ضریب ده افزایش مییابد. اما همانگونه که نشان داده شده، در سیستم شمارهگذاری BCD، وزن باینری هر رقم با ضریبی از دو افزایش پیدا میکند. لذا اولین رقم وزنی معادل ۱ (۲۰)، دومین رقم وزنی معادل ۲ (۲۱)، سومین رقم وزنی معادل ۴ (۲۲) و چهارمین رقم وزنی معادل ۸ (۲۳) دارد.
جدول زیر رابطهی بین اعداد دهدهی و ارقام BCD وزندار را نشان میدهد.
جدول صحت BCD
| عدد دهدهی | کد BCD 8421 |
| ۰ | ۰۰۰۰ ۰۰۰۰ |
| ۱ | ۰۰۰۰ ۰۰۰۱ |
| ۲ | ۰۰۰۰ ۰۰۱۰ |
| ۳ | ۰۰۰۰ ۰۰۱۱ |
| ۴ | ۰۰۰۰ ۰۱۰۰ |
| ۵ | ۰۰۰۰ ۰۱۰۱ |
| ۶ | ۰۰۰۰ ۰۱۱۰ |
| ۷ | ۰۰۰۰ ۰۱۱۱ |
| ۸ | ۰۰۰۰ ۱۰۰۰ |
| ۹ | ۰۰۰۰ ۱۰۰۱ |
| ۱۰ (۱+۰) | ۰۰۰۱ ۰۰۰۰ |
| ۱۱ (۱+۱) | ۰۰۰۱ ۰۰۰۱ |
| ۱۲ (۱+۲) | ۰۰۰۱ ۰۰۱۰ |
| … | … |
| ۲۰ (۲+۰) | ۰۰۱۰ ۰۰۰۰ |
| ۲۱ (۲+۱) | ۰۰۱۰ ۰۰۰۱ |
| ۲۲ (۲+۲) | ۰۰۱۰ ۰۰۱۰ |
| ….. | |
همانگونه که میبینیم، کد ۸۴۲۱ BCD همان وزنهای ارقام باینری است که در آن هر رقم دهدهی با معادل باینری چهار بیتی آن نمایش داده میشود.
تبدیل دهدهی به BCD
با توجه به جدول بالا قوانین تبدیل اعداد دهدهی به BCD، شباهت بسیار زیادی به قوانین تبدیل اعداد هگزادسیمال به باینری دارد. ابتدا، ارقام وزندار عدد دهدهی را جدا کرده و سپس معادل باینری هر رقم را در قالب چهار بیت مینویسیم. با کنار هم قرار دادن بیتهای مربوط به هر رقم، کد ۸۴۲۱ BCD عدد به دست میآید.
مثال شماره ۱ کد BCD
با استفاده از جدول بالا، اعداد دهدهی زیر را به معادل ۸۴۲۱ BCD آنها تبدیل کنید.
۸۵۱۰ = ۱۰۰۰ ۰۱۰۱ (BCD)
۵۷۲۱۰ = ۰۱۰۱ ۰۱۱۱ ۰۰۱۰ (BCD)
۸۵۷۹۱۰ = ۱۰۰۰ ۰۱۰۱ ۰۱۱۱ ۱۰۰۱ (BCD)
توجه کنید که عدد باینری تولید شده بعد از تبدیل هر رقم دهدهی، باید چهار بیت باشد. اگر معادل باینری رقمی کمتر از چهار بیت بود، در سمت چپ آن به تعداد مورد نیاز صفر قرار میدهیم تا به چهار بیت برسد.
مشاوره رایگان
تبدیل BCD به دهدهی
تبدیل BCD به دهدهی دقیقاً عکس عملیات قبلی است. تنها لازم است عدد باینری را به گروههای چهار بیتی تقسیم کرده و با شروع از کم ارزشترین رقم، معادل دهدهی هر یک از گروههای چهار بیتی را بنویسیم. در صورت نیاز برای تشکیل یک گروه چهار بیتی کامل، در سمت چپ عدد صفرهای اضافی قرار میدهیم. به عنوان مثال، عدد ۱۱۰۱۰۱۲ به ۰۱۰۱۲ 0011 یا ۳۵۱۰ دهدهی تبدیل میشود.
مثال شماره ۲ کد BCD
اعداد باینری ۱۰۰۱۲، ۱۰۱۰۲، ۱۰۰۰۱۱۱۲ و ۱۰۱۰۰۱۱۱۰۰۰.۱۰۱۲ را به معادل دهدهی آنها تبدیل کنید.
۱۰۰۱۲ = ۱۰۰۱BCD = ۹۱۰
خطا میدهد، زیرا معادل ۱۰۱۰ است که یک عدد BCD غیرمجاز است = 1010۲
۱۰۰۰۱۱۱۲ = ۰۱۰۰ ۰۱۱۱BCD = ۴۷۱۰
۱۰۱۰۰۱۱۱۰۰۰.۱۰۱۲ = ۰۱۰۱ ۰۰۱۱ ۰۰۰۱.۱۰۱۰BCD = ۵۳۸.۶۲۵۱۰
تبدیل عدد BCD به دهدهی یا دهدهی به BCD معمولاً راحت است و پیچیدگی خاصی ندارد؛ البته باید همواره به یاد داشت هرچند که اعداد BCD با بیتهای ۰ و ۱ نشان داده میشوند، اما در واقع اعداد دهدهی هستند و نه باینری. درک نمایش BCD یک عدد دهدهی بسیار اهمیت دارد، زیرا لازم است که سیستمهای مبتنی بر میکروپروسسور رایج، از اعداد دهدهی استفاده کنند.
اگرچه کدگذاری (code) و کدگشایی (decode) اعداد BCD بسیار راحت است، اما روش مقرون به صرفهای برای ذخیرهی اعداد به شمار نمیروند. در کدگذاری یا انکود کردن (encoding) اعداد دهدهی به ۸۴۲۱ BCD، همواره تعداد بیتهای لازم برای نمایش یک عدد دهدهی فرضی، بیشتر از تعداد بیتهای لازم برای انکود کردن باینری همان عدد است.
به عنوان مثال، معادل باینری یک عدد دهدهی سه رقمی (از ۰ تا ۹۹۹) حداکثر ۱۰ بیت خواهد بود (۱۱۱۱۱۰۰۱۱۱۲)، اما برای نمایش BCD همان عدد به حداقل ۱۲ بیت نیاز داریم (۰۰۱۱۱۱۱۰۰۱۱۱BCD).
نکتهی دیگر اینکه انجام عملیات ریاضی روی اعداد BCD ممکن است مشکلاتی را ایجاد کند، زیرا ارقام نمیتوانند از ۹ بزرگتر باشند. لذا ممکن است با جمع دو عدد دهدهی در سیستم BCD، بیت نقلی carry) 1) تولید شود که در اینگونه مواقع باید آن را به گروه چهار بیتی بعدی اضافه کنیم.
اگر حاصل جمع بیت نقلی با چهار بیت باینری کوچکتر مساوی ۹ (۱۰۰۱) باشد، رقم BCD متناظر نیز بدون اشکال است. اما اگر این حاصل جمع از ۹ بزرگتر باشد، یک رقم BCD غیرمجاز تولید میکند. در نتیجه ایدهی بهتری است که ابتدا اعداد BCD را به باینری تبدیل کرده، عملیات جمع را بر روی اعداد باینری انجام داده و در آخر نتیجهی به دست آمده را دوباره به BCD تبدیل کنیم.
با وجود این محدودیتها، در میکروالکترونیک و سیستمهای کامپیوتری استفاده از اعداد BCD بسیار رایج است، مخصوصاً برای نمایش یک یا چند رقم بر روی LED یا LCD های هفت قسمتی که به آنها «سونسگمنت» (۷-segment) نیز گفته میشود. IC های بسیار متنوعی نیز برای این منظور ساخته شدهاند که ورودی BCD گرفته یا خروجی BCD تولید میکنند.
یکی از پرکاربردترین این آیسیها 74LS90 نام دارد که یک شمارنده/تقسیمکنندهی آسنکرون با خروجی BCD است. این آیسی از دو شمارندهی مجزا از هم «تقسیم بر ۲» و «تقسیم بر ۵» تشکیل شده که با ترکیب آنها میتوان یک شمارندهی «تقسیم بر ۱۰» ساخت. یک آیسی دیگر 74LS390 است که در واقع از دو آیسی 74LS90 ساخته شده و میتوان بهگونهای آن را تنظیم کرد که خروجی BCD تولید کند.
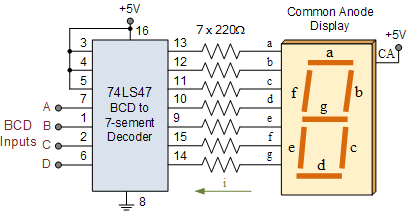
پرکاربردترین IC های دیکود BCD عبارتند از 74LS47 و 74LS48 که دیکودر BCD به کد سونسگمنت (7segment) و درایور یا راهانداز آن هستند. 74LS48 یک کد BCD چهار بیتی را گرفته و آن را به کد سونسگمنت لازم برای راهاندازی یک نمایشگر LED سونسگمنت تبدیل میکند. اگرچه این دو آیسی تقریباً شبیه به یکدیگر عمل میکنند، اما تفاوتهایی نیز دارند. خروجیهای 74LS47 به صورت active-low بوده (یعنی اگر خروجی فعال باشد، صفر خواهد بود) و برای راهاندازی نمایشگرهای آند-مشترک استفاده میشود؛ اما خروجیهای 74LS48 به صورت active-high بوده (یعنی اگر خروجی فعال باشد، یک خواهد بود) و در راهاندازی نمایشگرهای کاتد-مشترک کاربرد دارد.
آیسی دیکودر BCD
خلاصه
در این آموزش دیدیم که BCD یا Binary Coded Decimal در حقیقت نمایش یک رقم دهدهی با ۴ بیت باینری است؛ به این صورت که هر رقم دهدهی صحیح یا اعشاری، با معادل باینریش جایگزین میشود. کد BCD برای نمایش ۱۰ رقم دهدهی ۰ تا ۹، از چهار بیت استفاده میکند.
لذا مثلاً برای نمایش اعداد دهدهی بازهی ۰ تا ۹ (یک رقم) به ۴ بیت (یک نیبل)، اعداد دهدهی بازهی ۰ تا ۹۹ (دو رقم) به ۸ بیت (یک بایت) و اعداد دهدهی بازهی ۰ تا ۹۹۹ (سه رقم) به ۱۲ بیت نیاز داریم و الی آخر. همانگونه که میبینید تنها با استفاده از یک بایت (۸ بیت) میتوان اعداد BCD در بازهی ۰۰ تا ۹۹ را ذخیرهسازی کرده و نمایش داد. به این عدد دو رقمی «BCD بستهبندی شده» (packed BCD) نیز گفته میشود.
کد BCD استاندارد معمولاً همان کد وزندار BCD 8421 است که ۸، ۴، ۲ و ۱ نشاندهندهی ترتیب و وزن بیتهای عدد با شروع از پر ارزشترین بیت (MSB) تا کم ارزشترین بیت (LSB) است. وزن هر یک از بیتهای کد BCD با توجه به موقعیت آنها برابرست با ۲۳ = 8، ۲۲ = 4، ۲۱ = 2 و ۲۰ = 1.
بزرگترین مزیت سیستم BCD در این است که در مقایسه با سیستمهای باینری محض، سیستم سریعتر و مؤثرتری برای تبدیل اعداد دهدهی به باینری به حساب میآید. اگرچه عدم به کارگیری شش وضعیت چهار بیتی ۱۰ تا ۱۶، از محبوبیتهای کد BCD میکاهد، اما کماکان کاربردهای بسیار مهمی در نمایشگرهای دهدهی دارد.
مشاوره پیش از ثبت نام
جهت اطلاع از جزئیات و شهریه دوره ها با ما در ارتباط باشید.مقالات مرتبط