میدان مغناطیسی

در حالت کلی می‌توان این اصول را به دو بخش اصلی فیزیک الکتریسیته و مغناطیس تقسیم‌بندی کرد.

مقدمه

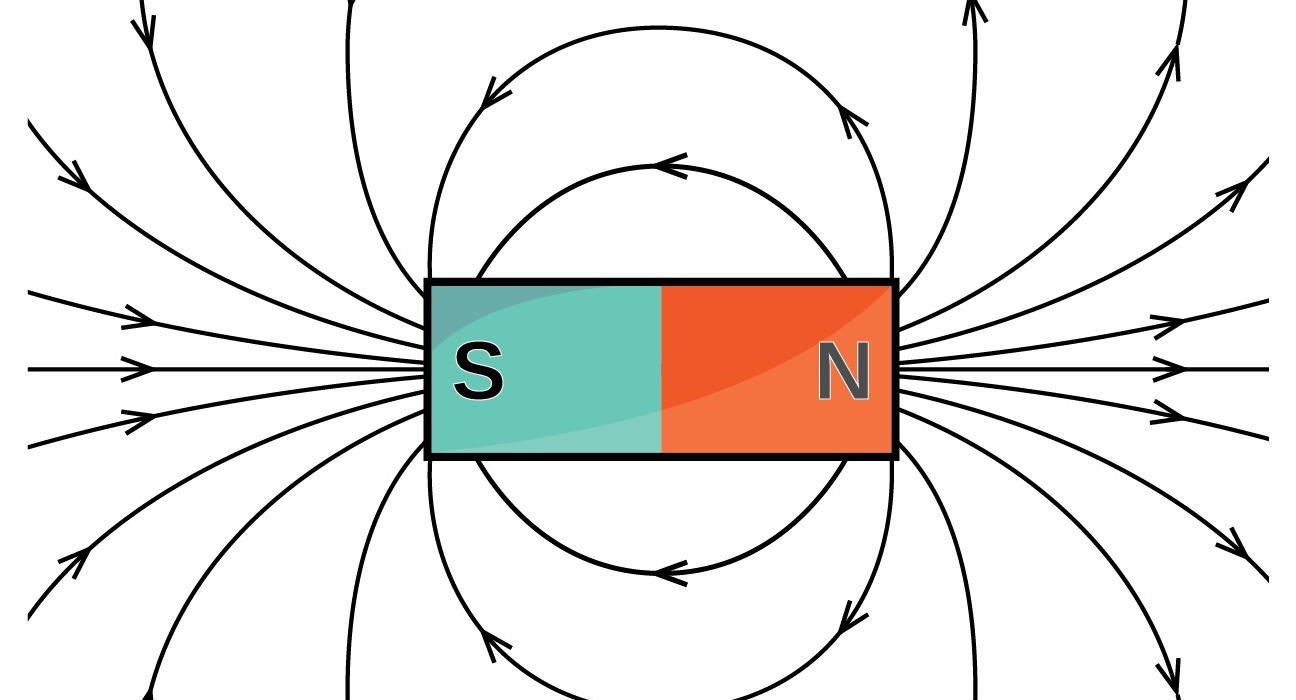
همان‌طور که بیان شد، یک ذره باردار می‌تواند در فضای اطراف خود میدانی الکتریکی ($$\overrightarrow{E}$$) ایجاد کند. به همین صورت، آهنربایی کوچک نیز می‌تواند اطراف خود میدانی مغناطیسی ایجاد کند. میدان مغناطیسی نیز همانند نسخه الکتریکی خود یک بردار است که آن را با $$\overrightarrow{B}$$ نشان می‌دهند. مطابق با شکل زیر می‌توان با حرکت دادن قطب‌نما در نزدیکی یک آهنربا، جهت میدان مغناطیسی را معلوم کرد.

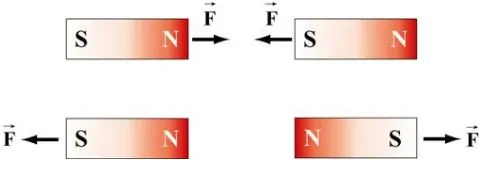
هر آهنربا دارای دو قطب است که آن‌ها را شمال (N) و جنوب (S) می‌نامیم. میدان‌های مغناطیسی در قطب‌ها بیشترین مقدار خود را دارند. همواره خطوط میدان مغناطیسی از N خارج شده و به S وارد می‌شود. تجربه نیز نشان می‌دهد که دو قطب مشابه یکدیگر را دفع و مخالف همدیگر را جذب می‌کنند. در شکل زیر، این دو حالت نشان داده شده است.

برخلاف بار‌های الکتریکی که می‌توانند فقط مثبت یا منفی باشند، ذرات مغناطیسی همواره دارای یک قطب N و یک قطب S هستند. در حقیقت نمی‌توان با جدا کردن یک جسم مغناطیسی قطب‌های آن را از هم جدا کرد. در شکل زیر می‌بینید که قطب‌های یک آهنربا پس از دو بخش شدن ثابت مانده‌اند.

میدان مغناطیسی به چه شکل تعریف می‌شود؟ برای پاسخ به این سوال در ابتدا اجازه دهید تا تعریف میدان الکتریکی را مرور کنیم. در مبحث میدان الکتریکی $$\overrightarrow{E}$$

، آن را به صورت نیروی ایجاد شده در واحد بار الکتریکی، به شکل زیر تعریف کردیم.

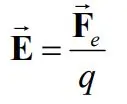
در حقیقت برای تعریف میدان نیاز به بار آزمون داشتیم؛ آیا برای تعریف میدان هم نیاز به دوقطبی مغناطیسی فرضی داریم؟

تعریف میدان مغناطیسی

به‌منظور تعریف میدان مغناطیسی در یک نقطه، مطابق با شکل زیر بار q را تصور کنید که با سرعت $$\overrightarrow{v}$$

در میدان مغناطیسی برابر با $$\overrightarrow{B}$$

در حال حرکت کرد.

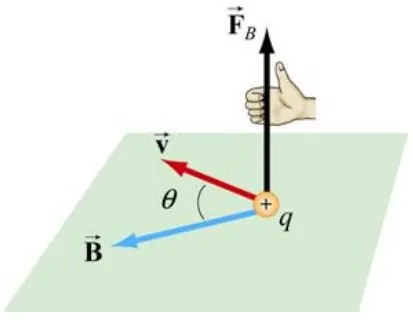
با توجه به آزمایش‌های صورت گرفته اتفاقات زیر دیده شده است.

1. نیرویی مغناطیسی ($$\overrightarrow{F_B}$$

• ) به ذره وارد می‌شود که اندازه آن متناسب با v و q است.
• اندازه و جهتِ $$\overrightarrow{F_B}$$

وابسته به دو کمیت $$\overrightarrow{v}$$ و $$\overrightarrow{B}$$

• است [با افزایش هرکدام از این دو کمیت، نیروی وارد شده به ذره نیز افزایش می‌یابد].
• نیروی مغناطیسی $$\overrightarrow{F_B}$$

3. در حالتی که بردار‌های v و B در یک جهت هستند، برابر با صفر است. هم‌چنین مطابق با شکل ۱، بردار نیروی وارد شده به ذره، بر صفحه تشکیل شده از دو بردار v و B عمود است. هم‌چنین اندازه نیرو به زاویه بین بردار سرعت و میدان مغناطیسی وابسته است؛ در حقیقت با افزایش Sin θ اندازه این نیرو نیز افزایش می‌یابد.
4. هنگامی که علامت بار q عوض می‌شود، جهت نیروی وارد شده به آن نیز عکس می‌شود.

اگر با مفاهیم ضرب داخلی و ضرب خارجی آشنا باشید، متوجه خواهید شد، مشاهدات بالا نشان می‌دهد که نیروی وارد شده به ذره را می‌توان با استفاده از رابطه زیر نشان داد.

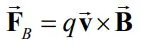
با توجه به رابطه بالا اندازه نیروی وارد شده به بار مفروض برابر است با:

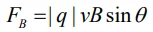
واحد میدان مغناطیسی در سیستم SI، تسلا (T) نامیده می‌شود. در حقیقت ۱ تسلا برابر است با:

البته در بعضی موارد از واحد دیگری تحت عنوان گاوس نیز برای نشان دادن میدان مغناطیسی استفاده می‌شود. در حقیقت ۱T=10^۴G در نظر گرفته می‌شود. با توجه به رابطه ۱، نیروی ناشی از میدان مغناطیسی همواره به میدان مغناطیسی و جهت حرکت بارهای الکتریکی عمود است. در حقیقت با استفاده از نیروی مغناطیسی نمی‌توان سرعت یک بار را در راستای حرکتش کم یا زیاد کند. هم‌چنین با توجه به رابطه زیر هیچگاه این نیرو کاری روی ذره باردار انجام نخواهد داد.

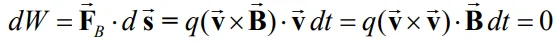
نیرو و گشتاور وارد به سیم حامل جریان

در بالا گفتیم که حرکت ذره در میدان مغناطیسی منجر به وارد شدن نیروی F_B به آن می‌شود. حال سیمی را تصور کنید که حاوی جریان الکتریکی است. در حقیقت این جریان، مجموعه‌ای از ذرات هستند که در سیم در حال حرکت‌اند. از این رو اگر این سیم را در میدانی مغناطیسی قرار دهید، نیرویی به آن وارد خواهد شد.

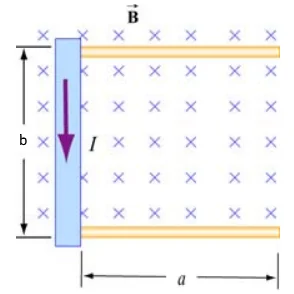
برای بدست آوردن این نیرو مطابق با شکل زیر سیمی را تصور کنید که بین دو قطب مغناطیسی قرار گرفته است. همان‌طور که در شکل نیز مشخص شده، میدان B با استفاده از نقاطی نشان داده شده است. دلیل این نقاط این است که جهت میدان عمود به صفحه در نظر گرفته شده.

مطابق با شکل بالا مشاهده می‌شود که اگر جهت جریان به سمت پایین باشد، سیم به سمت چپ منحرف می‌شود و اگر جهت جریان به سمت بالا باشد، سیم به سمت راست منحرف می‌شود. جهت بدست آوردن اندازه این نیرو مطابق با شکل زیر در ابتدا بخشی از سیم به طول l و سطح مقطع A را در نظر بگیرید.

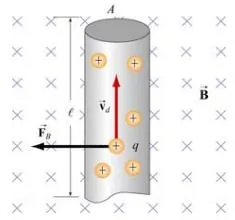
به یاد داشته باشید که جهت بردار‌های میدانی که به سمت داخل صفحه هستند با علامت × و جهت بردار‌های به سمت بیرون با نقطه نشان داده می‌شود.

فرض کنید که سرعت میانگین ذرات برابر با $$\overrightarrow{v_d}$$

است. باری برابر با $$Q_{tot}=q\left(nAl\right)$$

در مقطع سیمِ در نظر گرفته شده قرار دارد. در این رابطه، n تعداد بارها در واحد حجم را نشان می‌دهد؛ در نتیجه نیروی وارد شده به سیم در این حالت برابر است با:

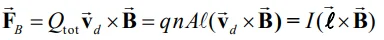
در رابطه بالا I=nqv_dA و $$\overrightarrow{l}$$

برداری به اندازه l است که هم‌جهت با مسیر حرکت جریان الکتریکی است. برای یک سیم، نیروی کلی وارد به آن را می‌توان با جمع‌ زدن نیروهای وارد به بخش‌های مختلفش بدست آورد. در ابتدا مطابق با شکل زیر دیفرانسیلِ طولِ سیم را برابر با بردار $$\overrightarrow{ds}$$

در نظر بگیرید.

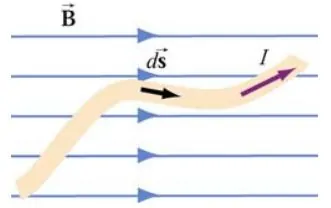
با توجه به رابطه ۲ می‌توان نیروی وارد به این دیفرانسیل را بصورت زیر نوشت:

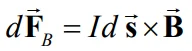
بنابراین نیروی وارد شده به کل سیم برابر است با:

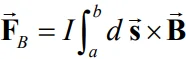
در رابطه بالا a و b بازه‌ای از سیم را نشان می‌دهند که می‌خواهیم نیروی مغناطیسی وارد به آن را محاسبه کنیم. برای مثال مطابقِ تصویر زیر فرض کنید که سیمی به شکل منحنی در میدانِ $$\overrightarrow{B}$$

قرار گرفته.

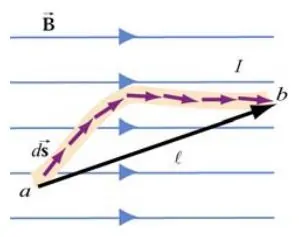
با استفاده از رابطه زیر می‌توان نیروی وارد به سیم مفروض را بدست آورد.

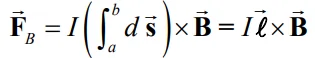
توجه داشته باشید که در رابطه بالا $$\overrightarrow{l}$$

برداری از نقطه a تا b است. حال فرض کنید که می‌خواهیم نیروی وارد به سیم بسته‌ِ شکلِ زیر را بدست آوریم.

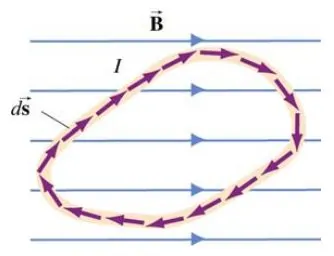
نیروی وارد شده به سیم بالا برابر است با:

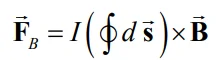
با توجه به این که انتگرال روی یک مسیر برداری بسته صفر است ($$\oint \overrightarrow{ds}=\mathrm{۰}$$

)، در نتیجه حاصل انتگرال بالا نیز برابر با صفر خواهد بود. جهت درک بهتر مفهوم بالا به مثال زیر توجه کنید.

مثال ۱

مطابق با تصویر زیر سیمی به شکل نیم‌دایره را تصور کنید که در میدان $$\overrightarrow{B}$$

قرار گرفته است. جریان موجود در سیم برابر با I و جهت آن به صورت پادساعتگرد است.

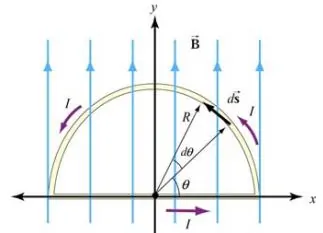
با این فرضیات نیروی وارد به سیم مفروض را بدست آورید؟

برای بدست آوردن نیروی مذکور در ابتدا بایستی میدان مغناطیسی را بصورت برداری بیان کرد؛ بردار میدان مغناطیسی برابر است با:

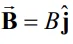
فرض کنید نیروهای $$\overrightarrow{F_{\mathrm{۱}}}$$

و $$\overrightarrow{F_{\mathrm{۲}}}$$

به ترتیب نیروی وارد شده به سیم قرار گرفته رو محور x و نیروی وارد به نیم‌دایره هستند. با توجه به تعریف، نیروی وارد شده به سیم قرار گرفته روی محور x برابر است با:

توجه داشته باشید که بردار k جهت عمود به صفحه و رو به بیرون را نشان می‌دهد. به همین صورت بمنظور محاسبه نیروی $$\overrightarrow{F_{\mathrm{۲}}}$$

در ابتدا بایستی $$\overrightarrow{ds}$$

را به صورت برداری مطابق با رابطه زیر بیان می‌کنیم:

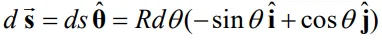
بنابراین دیفرانسیل $$\overrightarrow{F_{\mathrm{۲}}}$$

برابر است با:

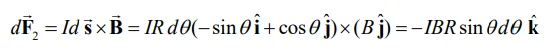
با انتگرال‌گیری از رابطه بالا روی کل نیم‌ دایره داریم:

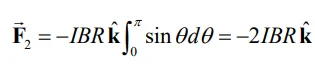
با جمع کردن نیروی $$\overrightarrow{F_{۱}}$$

و $$\overrightarrow{F_{\mathrm{۲}}}$$

، نیروی خالص بدست آمده روی کل سیم به شکل زیر بدست می‌آید.

بنابراین همان‌گونه که محاسبه شد نیروی وارد شده به کل سیم برابر با صفر بدست آمد. بنابراین همان‌گونه که در بالا نیز بیان کردیم، نیروی وارد به یک سیم بسته که در میدان مغناطیسی قرار گرفته، صفر است.

گشتاور وارد به حلقه بسته قرار گرفته در میدان مغناطیسی

با وجود آن‌که نیروی خالص وارد شده به یک حلقه بسته حاوی جریان برابر با صفر است، اما با قرار دادن آن در یک میدان مغناطیسی، گشتاوری به حلقه وارد خواهد شد. برای تحلیل این موضوع در ابتدا مطابق با شکل زیر حلقه‌ بسته‌ای، حاوی جریان I را فرض کنید که در میدان مغناطیسی $$\overrightarrow{B}$$

قرار گرفته است.

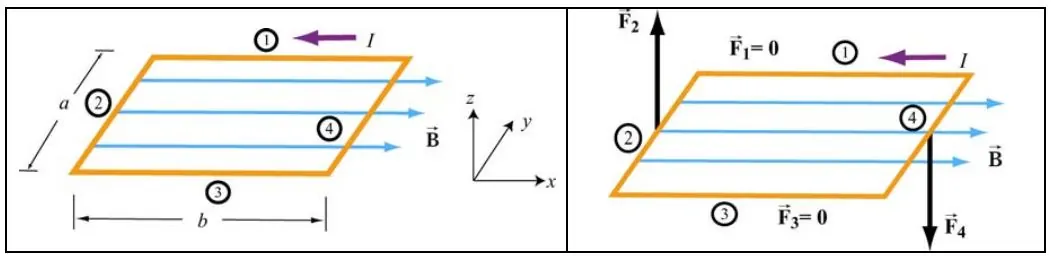
با توجه به جهت میدان مغناطیسی و جهت جریان در هر بخش از سیم، نیروی کل وارد شده به آن برابر است با:

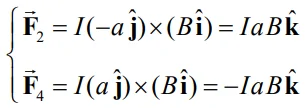
در رابطه بالا نیروی F_۲ رو‌به بالا و نیروی F_۴ رو به پایین است.هم‌چنین توجه داشته باشید که دلیل صفر بودن نیروی وارد به بخش ۱ و ۳ این‌ است که در قسمت‌های مذکور، جریان الکتریکی و میدان مغناطیسی با یکدیگر هم‌جهت هستند. با توجه به این‌که دو نیروی غیر صفر در خلاف جهت هم هستند، بنابراین گشتاور خالصی را به سیم وارد خواهند کرد که منجر به دوران کل حلقه حول محور y خواهد شد. از این رو گشتاور حول مرکز حلقه برابر است با:

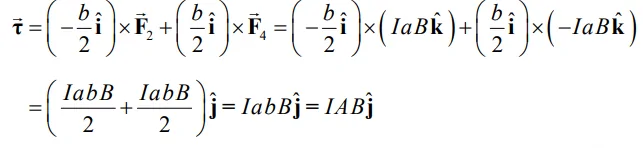
در رابطه بالا A=ab برابر با مساحت سطح درون حلقه است. هم‌چنین با توجه به مثبت بودن علامت گشتاور، جهت چرخش آن به‌صورت ساعتگرد و حول محور y خواهد بود. مرسوم است که برای نشان دادن مساحت، از بردار $$\overrightarrow{A}=A\hat{n}$$

استفاده می‌شود که در آن $$\hat{n}$$ نشان دهنده بردار عمود به صفحه است. در این مسئله $$\hat{n}=+\hat{k}$$

در نظر گرفته شده. با توجه به مفاهیم بیا‌ن شده رابطه ۳ را می‌توان به شکل برداری که در زیر آمده بیان کرد:

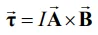
با توجه به رابطه بالا می‌توان فهمید در حالتی که میدان B عمود به صفحه باشد، بیشترین گشتاور ممکن به حلقه وارد خواهد شد. در حالتی عمومی‌تر فرض کنید که مطابق شکل زیر زاویه $$\hat{n}$$

و بردار $$\overrightarrow{B}$$ برابر با $$\theta$$

است.

بردار‌های $$\overrightarrow{r_{\mathrm{۲}}}$$

و $$\overrightarrow{r_{۴}}$$

دقیقا عکس هم هستند. از این رو می‌توان گفت:

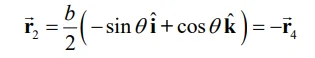
با توجه به نیرو‌های نشان داده شده در شکل بالا، گشتاور خالص وارد شده به سیم برابر است با:

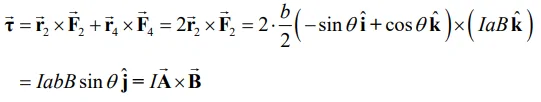
از این رو اگر با N حلقه روبرو باشیم، اندازه گشتاور برابر است با:

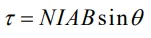
مقدار $$\frac{N}{\overrightarrow{A}}$$

برابر «گشتاور دوقطبی مغناطیسی» (Magnetic Dipole Moment) نامیده می‌شود و آن را با $$\mu$$

نمایش می‌دهند. این کمیت برداری، برابر است با:

همان‌طور که در شکل زیر نشان داده شده، بردار‌های $$\overrightarrow{\mu }$$

و $$\overrightarrow{A}$$

در یک جهت هستند.

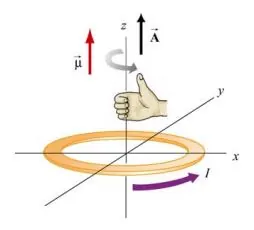
جهت بردار $$\mu$$

را – مطابق با شکل بالا – می‌توان با استفاده از قانون دست راست تعیین کرد. در حقیقت بایستی انگشتان دست خود را در جهت جریان بچرخانید و در این حالت انگشت شست شما، جهت $$\overrightarrow{\mu }$$ را نشان می‌دهد. ماهیت رابطه بالا نشان می‌دهد که واحد $$\mu$$

برابر با A.m^۲ است. هم‌چنین گشتاور وارد به حلقه با استفاده از گشتاور دوقطبی مغناطیسی، مطابق با رابطه زیر قابل نمایش است.

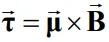
کار انجام شده توسط گشتاور وارد به حلقه منجر به افزایش انرژی پتانسیل (U) می‌شود.در حالتی که این حلقه از زاویه θ_۰ تا θ دوران می‌کند، تغییرات انرژی آن برابر با کار انجام شده توسط میدان مغناطیسی است که با استفاده از رابطه زیر قابل محاسبه است.

اگر انرژی پتانسیل در حالت اولیه برابر با صفر فرض شود (U_۰)، انرژی پتانسیل حلقه‌ای که در زاویه θ، در میدان B قرار گرفته با استفاده از رابطه زیر بیان می‌شود:

مثال ۲: میله در حال دوران روی ریل

مطابق شکل زیر میله‌ای به جرم m و شعاع R را تصور کنید که روی ریلی قرار گرفته و فاصله میان ریل برابر با b و طول آن‌ برابر با a است. میله جریان I را در خود داشته و می‌تواند آزادانه روی ریل حرکت کند. هم‌چنین $$\overrightarrow{B}$$

به‌صورت عمود به صفحه و به سمت داخل آن در نظر گرفته شده. اگر در ابتدا میله در حالت سکون باشد، سرعت نهایی آن وقتی به انتهای ریل می‌رسد، چقدر خواهد بود؟

با توجه مفاهیم بیان شده در بالا، نیروی وارد به میله با استفاده از رابطه زیر بدست می‌آید.

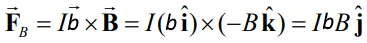
کار انجام شده توسط نیروی مغناطیسی برابر است با:

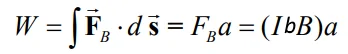
با استفاده از رابطه کار-انرژی، کار انجام شده روی میله، منجر به افزایش انرژی جنبشی آن خواهد شد و یا به بیانی ریاضیاتی:

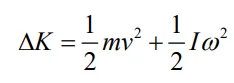
عبارت اول سمت راست معادله بالا انرژی جنبشی خطی و عبارت دوم نشان دهنده انرژی دورانی آن است. از مطلب لختی دورانی می‌دانیم که لختی دورانی میله‌ای به شعاع R حول محورش برابر با $$I=\frac{m{R}^{\mathrm{۲}}}{\mathrm{۲}}$$

و رابطه بین سرعت خطی و دورانی میله برابر با ω=v/R است. با توجه به این دو مقدار و جایگذاری آن در رابطه بالا داریم:

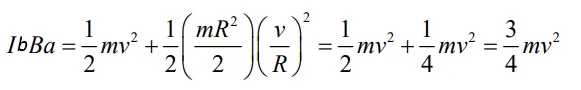
با حل معادله بالا، سرعت خطی میله در نقطه a برابر است با:

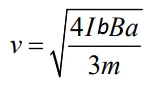
مثال ۳: میله معلقِ قرار گرفته در میدان مغناطیسی

میله‌ای به چگالی λ و طول l را در نظر بگیرید که توسط دو سیم به صورت معلق نگه داشته شده است. این دو سیم بخشی از یک مدار بسته را تشکیل می‌دهند که حامل جریان I است. در همین حال مطابق شکل زیر میدان B در ناحیه‌ای از فضا به سمت بیرونِ صفحه اعمال می‌شود. اگر نیروی کشش در دو سیم نگه‌دارنده صفر باشند، جهت و اندازه جریان الکتریکی چقدر است؟

بدیهی است که برای صفر بودن کشش دو سیم، نیروی ناشی از میدان مغناطیسی بایستی به سمت بالا و اندازه آن برابر با نیروی وزن باشد. نیروی $${\overrightarrow{F}}_B$$

برابر است با:

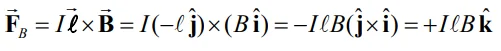
با برابر قرار دادن نیروی بالا با نیروی گرانش داریم:

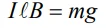
با مرتب سازی رابطه بالا بر حسب I، جریان الکتریکی برابر با مقدار زیر بدست می‌آید.

هم‌چنین برای این‌که نیروی مغناطیسی رو به بالا باشد، با استفاده از قانون دست راست، جهت جریان به سمت چپ بدست می‌آید. در حقیقت با قرار دادن انگشتان خود در جهت جریان و منحرف کردن آن‌ها در جهت میدان مغناطیسی، جهت انگشت شستمان جهت بالا را نشان می‌دهد که همان جهت نیروی وارد شده به میله است.